Daniel's Web-Page
Combinations and Permutations
Contents
Blaise Pascal
Pascal's Problem
The Fundamental Counting Principle
The Tree Diagram
Travel Plans
Jargon
Leonard Euler
Permutations and Factorial
Tri-Ominos
Ringing the Changes
Combinations
Rearranging Letters
Probability and Statistics
Dice Chart
Simple Dice Games
Backgammon
St. Olav's Random Miracle
Introduction
Combinations and permutations are used to determine probability, which can be used in real-life situations like predicting the weather, knowing whether to hit or stay in a game of blackjack and many many others. This book starts at the beginnings of probability with the assumption that the reader understands basic arithmetic and how to use fractions. From these basics, the reader is taken through the steps of how to calculate the number of outcomes of any event if enough data is given. From there the reader moves on to finding the probability of similar events. The reader will be submersed in the formulas for factorial, summation, combinations and permutations and how to construct probability equations. This book gives the reader enough data for predicting basic events such as the flip of a coin, or the roll of the dice or the likely number spun with a roulette wheel. There is an appendix that is full of problems covering the material taught throughout this book. Use this to test your knowledge of combinations and permutations.
Blaise Pascal
Blaise Pascal was a renowned mathematician most famous for the discovery of Pascal’s triangle. He is also famous for a piece of logic named “Pascal’s Wager”. A friend asked him if someone should believe in God. After much thought, Pascal replied that everyone should live their lives as if they believed in God because it is not worth the risk of going to hell, and there is nothing to lose by living a life of virtue. He was born in Clermont, France in 1623. He was not a healthy child and was forbidden by his physician to study math. Pascal was also not allowed to go to regular school, so his father, Etienne, hired a private tutor for him.
Pascal later heard his friends talking about geometry and was intrigued. He asked his tutor to explain this to him, but his tutor refused. With much persistence, his tutor finally said, “it is a way to solve problems using ratios”. This, however, only increased Pascal’s interest. He then snuck into his fathers’ study (who happened to be a mathematician) as often as he could to read books and his father’s notes. By the age of 12, he managed to teach himself Euclidean Geometry. His father then gave in to Pascal’s wishes, and the family moved to Paris where Pascal joined a math discussion group. At the age of 14, he became one of the more prominent figures of the group. Pascal’s health was still frail, and his physician suggested that Pascal set aside his books and pursue a life of frivolity like the other youths of Paris. This surprisingly did not help.
Pascal reached his pinnacle of math fame at the age of 20 although his nights were spent either gambling or getting drunk. When he was 30, he moved to the countryside and began his most productive year of mathematics. In 1654, he was involved in a bad carriage accident. During the accident, he had a vision of God. He miraculously survived and he immediately gave up mathematics to live his life as a monk. He later died of organ failures in 1662.
Pascal’s triangle can be used to solve combination problems. It is formed by starting with a one, under and to each side of that one another one is placed. Now under and in the middle of two numbers write the sum of the two numbers above it. The triangle is surrounded by zeros, so the edge of the triangle is always 1 + 0 = 1. Pascal’s triangle is on the next page. The triangle that is colored in is based off of Pascal’s triangle. Each color represents a number from zero to six. 0 = dark blue, 1 = black, 2 = red, 3 = orange, 4 = yellow, 5 = green, and 6 = light blue. Each hex’s number is divided by seven, and the remainder determines what color is put into it. For example, if the triangle’s number is four, then it is filled in with the color yellow because the remainder is four. If the triangle’s number is fifteen, then fifteen divided by seven is two with a remainder of one, so the triangle is colored in with black.
Pascal's Problem
One of Pascal’s good friends, Chevalier de Mere, was gambling with another one of his friends. The game was played to three points and the score was at 1:2 with Chevalier behind when he received an urgent message summoning him home. Since there was a considerable sum of money in the pot, there was some dispute as to how the pot should be split. After a heated argument, they decided to let their good friend the renowned mathematician Pascal decide what would be a fair way to split the pot.
Pascal based his answer on the probability of either of them winning the match. The game they were playing did not require much skill, so it was a simple matter to calculate what the likely outcome would be. In the next hand, Chevalier had a 1 / 2 probability of winning (either he wins or his opponent wins). In the hand after that, he still has a 1 / 2 chance of winning. So his overall odds of winning the match is 1 / 2 * 1 / 2 = 1 / 4. So the pot was split where Chevalier received one quarter of the pot and his opponent received three quarters of the pot. This result satisfied both parties and prevented a likely duel.
The Fundamental Counting Principle
The Fundamental counting Principle: To find the number of different ways of making several decisions in succession, multiply the number of choices that can be made in each decision.
So if the first decision has three choices, and the second decision has five choices, multiply three and five together to find the total number of ways of making the decision. An example of a practical application: there are three dice, how many total combinations of rolls are there? The first die can be a 1, 2, 3, 4, 5, or a six, which means there are six ways to make the first decision. There are also six ways to make the second decision (1, 2, 3, 4, 5, or 6) and six for the third decision. The total ways of making all the decisions is 6 * 6 * 6 = 256.
The following tree diagram shows a simple way for writing out each combination of a set. Later, there will be ways to calculate the number of different combinations in a set. The travel plan is an example a problem that uses the fundamental counting principle.
The Tree Diagram
Tree Diagrams are used to help visualize permutations, that is, how many different ways there are to rearrange a set. For example, say there are four people at a dinner party how many ways are there to arrange their seating order? To use the tree diagram, first assign each person a letter or number we’ll use A, B, C, and D. In the highest row, put A, B, C, and D. Under each letter attach every other letter that is not in use in the thread above it, so for C, put A, B, and D since C is already in use. Now Under each new letter, again write out every letter under it that is not in use by the thread above it, so for the thread B - D, write out A and C since they are not yet in use. Then continue this pattern until all the letters are used. The number of letters in the final row is the total number of permutations. The tree diagram looks like this:
Travel Plans
On a trip around the United States, Mr. and Mrs. Jones plan to travel from Portland to San Francisco to Los Angeles to New York to Chicago to Aspen in that order, before returning to Portland. The number of different airlines they can fly on is shown on the map. So the number of different ways they can travel through their whole trip is 3 * 3 * 2 * 3 * 2 * 2* 2 = 432 ways.
Jargon
Listed in the appendix is a chart of thirty words in three columns. If a word were taken from each column, they would make a phrase that sounds important but means nothing. An example of how three of these phrases would be used in a paragraph is below, the phrases are underlined:
To be a successful businessman, you must integrate a systematized monitored concept into your business cycle. Providing your human resources with functional third-generation hardware will increase your annual projected excess revenue. The shareholders of your company will be most impressed if you are able to develop a compatible management contingency.
Out of the list, how many different phrases is it possible to make? This is a direct example of the fundamental counting principle, there are ten options for the first word, ten for the next, and ten for the next, so the total number of possible phrases is: 10 * 10 * 10 = 1000.
Leonard Euler
Leonard Euler (1707 - 1783) attended a one-room schoolhouse in his youth. His teacher was an uptight man who was not sparing with the rod. One morning his teacher was having a hangover, he didn’t feel like teaching much and he assigned the class some busywork. He told his students to add up all the numbers from one to one hundred expecting this to keep the children occupied for quite some time. Half a minute later, Euler walks up to his teacher and says, "Please sir, can I have some more work." His teacher was outraged and shouted back, "Go back to your seat and finish the work I assigned you!" "But," Euler replied, "It was too easy, I’ve already finished it."
Euler obviously did not add each and every number. Instead, he found a formula, which he applied to all the numbers. The way to find the formula he used is to first break down the problem into simpler parts. So it would be easier to first find out how to add up all the numbers from one to ten. Written out, this would be: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = ?. What Euler noticed was that the sum of the first and last number (1 + 10 = 11) equals the sum of the second and second to last number (2 + 9 = 11), which also equals 3 + 8 and 4 + 7 and 5 + 6. There are five sets of sums (1 + 10, 2 + 9, 3 + 8, 4 + 7, 5 + 6) which happens to be ten (the final number) divided by two. So this agonizing addition problem turns into a simple multiplication problem. Just take the sum of the first and last number and multiply it by the last number divided by two. In a mathematical equation, this would be: (1 + 10) * (10 / 2) = 11 * 5 = 55.
This process is now called ‘summation’ which is written with the symbol 
. The symbol would be used in an equation like so: 101, which means to add all the numbers from one to ten. The original problem the teacher posed the students would be written mathematically as: 1001 = (1 + 100) * (100 / 2) = 101 * 50 = 5050.
Permutations and Factorial
The term ‘factorial’ is represented by an exclamation mark (!). This means to multiply the number that precedes it by every integer below it down to one. So four factorial (4!) is 4 * 3 * 2 * 1 = 24.
A permutation is an arrangement of a group of items in a specific order. For the three items A, B, and C, there are six permutations: ABC, ACB, BAC, BCA, CAB, and CBA. To find exactly how many permutations there are with three items the formula is simply: three factorial. This works because the first letter in the group can be any of the three items (A, B, or C). The next letter cannot be the same as the first, so there are only two items to choose from. The last place can only be chosen from one letter because the other two have already been used. For example, the first letter can be anything, say it is B, the next letter can be either A, or C, say it is A, the last letter now has to be C because the others have already been used. This means that the total number of permutations of any given set is the number of items in question, factorial (!).
Now if there were five items, how many different ways would there be to pick two items? The first place can be held by any of the five items. The second place then has only four items left. Thus there are 5 * 4 = 20 different ways of picking two out of five items. This process is written in shorthand as: 5P2, which means that out of five items, two are chosen in a specific order. The formula for this is nPr = n! / (n - r)!
A couple of examples of real-world applications of this are as follows:
1. How many ways are there to rearrange the letters of the word SCRAMBLE? There are eight different letters, so there are 8! (8 * 7 * 6 * 5 * 4 * 3 * 2 * 1) ways of rearranging them.
2. In how many ways can the first three moves in a game of tic-tac-toe be made? There are nine squares in which the first move can be made, there are eight for the second and seven for the third = 9 * 8 * 7 = 504. This is, by the way, 9P7. See the appendix, lesson two, for more problems.
Tri-Ominos
A tri-omino is a plastic triangle with numbers on each corner ranging from zero to five. 
Two tri-ominos are the same if, when oriented correctly, they have the same numbers at the same positions. However, two tri-ominos can be different even if they have the same numbers as long as there is no orientation that will place the same numbers at the same position. For example:
are different because there is no orientation that will line up the numbers from both tri-ominos.
A complete set of tri-ominos consists of every combination of numbers on a tile without making any duplicates. How many tri-ominos are in a complete set? The hard way to do this would be to list them all out keeping in mind which are duplicates and which aren’t. The mathematical way to solve this would be to break it up into smaller parts.
The first (and easiest) part would be the triples. There’s no need to find a formula because the only combinations are: 000, 111, 222, 333, 444, and 555 = 6. That’s the first part, which will be set aside for now.
The second part is the doubles. With them, 122, 212, and 221 are all the same because they can all be rotated to match each other, so the total number of combinations of tri-ominos with doubles is: the double, which can be anything (00, 11, 22, 33, 44, or 55) times the last number which cannot match the double (any of the remaining five numbers) this all equals: 6 * 5 = 30. Again this will be set aside for later.
The last and final part is the most difficult because the equation must take into consideration that 123 and 132 are different. The entire list of singles regardless of duplicates would be: the first number could be anything (6) * the second number which can’t match the first (5) * the third number which can’t match either of them (4) = 120 (this is by the way, 6P3, or 6! / 3!). Then this result must be divided by the number of ways each tri-omino can be oriented so that the same numbers would be on the same places, for instance, 123 can be oriented to form 231 and 321 which are all the same. So the original result is divided by three to get rid of all the duplicates. The entire equation for the singles is: 6P3 / 3 = (6! / 3!) / 3 = (6 * 5 * 4) / 3 = 120 / 3 = 40. Now add the results from each part to obtain the number of tri-ominos in a complete set. This is: 6 + 30 + 40 = 76.
Ringing the Changes
In many churches in Europe, they have an annual performance called “ringing the changes”. This is where the church rings their bells (usually five, but sometimes more) in every possible permutation exactly once. People from all over Europe come to these churches to listen to the performance. The director makes sure that no permutation is rung twice and every director has his own system to accomplish this. My class split up into several groups, and we all had to come up with our own systems for ringing the changes with four bells. Since there are only 24 permutations with four bells (4! = 4 * 3 * 2 * 1 = 24) it would be very easy to list out all the permutations and then while directing, simply read out each permutation. The list would look like this:
| 1234 | 1243 | 1324 | 1342 | 1423 | 1432 |
| 2134 | 2143 | 2314 | 2341 | 2413 | 2431 |
| 3124 | 3142 | 3214 | 3241 | 3412 | 3421 |
| 4123 | 4132 | 4213 | 4231 | 4312 | 4321 |
My group decided that this is not a very good system, because listing out all the permutations for five or six bells would be agonizing (5! = 5 * 4 * 3 * 2 * 1 = 120, while 6! = 720). We noticed a small pattern in the above chart. From left to right within a group, wherever possible, each number goes from smallest to biggest. It starts at 1234. The next group can’t be the same, so the last two numbers are switched, 1243. Then since the last two numbers can’t be switched again, the next number over (left) takes the next free spot. The two is the next number over, and it takes the spot next to it (moves to the right), while the other numbers remain in smallest to greatest order. So the third group in the series is: 1324. Now the last two numbers can be switched again (1342). Again, the last two numbers can’t be switched, so the next free number (the number which has not yet been used in the second spot, which is the four) is moved to the second spot and the other numbers remain in smallest to greatest form. The group is: 1423. The last two numbers are again switched forming 1432. This concludes the first row of groups which are all the permutations starting with one. The next row down is thought out in the same way as the first, except that the groups start with two. The same goes with the third and fourth row replacing the three and four respectively. With this thought-process, it is quite easy to lead the group without reading anything off paper.
Using five numbers is almost the same as using four numbers, where all that changes is the first number. The beginning of the chart of five-number permutations is as follows:
| 12345 | 12354 | 12435 | 12453 | 12534 | 12543 | ||||||||||
| 13245 | 13254 | 13425 | 13452 | 13524 | 13542 | ||||||||||
| 14235 | 14253 | 14325 | 14352 | 14523 | 14532 | ||||||||||
| 15234 | 15243 | 15324 | 15342 | 15423 | 15432 | ||||||||||
| 21345 | 21354 | 21435 | 21453 | 21534 | 21543 | ||||||||||
| 23145 | 23154 | 23415 | 23451 | 23514 | 23541 | ||||||||||
| 24135 | 24153 | 24315 | 24351 | 24513 | 24531 | ||||||||||
| 25134 | 25143 | 25314 | 25341 | 25413 | 25431 | ||||||||||
|
|||||||||||||||
| 51234 | 51243 | 51324 | 51342 | 51423 | 51432 | ||||||||||
| 52134 | 52143 | 52314 | 52341 | 52413 | 52431 | ||||||||||
| 53124 | 53142 | 53214 | 53251 | 53412 | 53421 | ||||||||||
| 54123 | 54132 | 54213 | 54231 | 54312 | 54321 | ||||||||||
The chart of fives is actually the same as the previous chart of four numbers, except that there is a five stuck before each number. This means that the thought-process for five bells is exactly the same as the thought-process for four numbers except for the first number. If the person playing the first bell in a chart steps forward a little (the person playing the two steps forward for the permutations that begin with two) then it would be extremely easy to think around them, to pretend that they are not there and just to run through the permutations for the remaining four.
Combinations
A combination is an arrangement of a group of items that is not in a specific order. Say there are three letters, A, A, and C, how many combinations of two letters are there? Since A(1)A(2) is the same as A(2)A(1) the formula is not 3P2. There are exactly 3P2 combinations minus the number of duplicates. For example, the list of all the permutations of two letters it thus: A(1)A(2), A(1)C, A(2)A(1), A(2)C, CA(1), CA(2). The number of combinations (not permutations) is this list minus all the doubles. There are three doubles, so the six total minus three equals three total combinations.
The formula for combinations is the same as the formula for permutations (n! / (n – r)!) except that somewhere, a term must be added to take out all the doubles. Since half of the list of permutations are doubles (2!) this formula can be divided by 2! Which is r!. So the final formula for combinations is: nCr = n! / ((n – r)! r!).
Pascal’s triangle can actually be used to solve simple combination problems. Simply go down to the row n, and over r places. For example, for 3C2, go down to the row with three in it, and over two spaces.
Here are some examples of how combinations can be used:
1. At the beginning of a every meeting of a very friendly club, each of the twenty members shakes hands with each of the others exactly once. How many handshakes are there in all, when every member is present? Out of twenty people, two people shake hands at a time, so the answer is 20C2 = 20! / (20 – 2)! 2! = 20 * 19 / 2 = 190
2. A new Senate Committee to be in charge of “Trivial Affairs” is to have three members. If all one hundred Senators are available to serve on it, how many different committees can be chosen? There are one hundred people in which three can be chosen and the order does not matter, so there are 100C3 different possible combinations of people that can be chosen for the committee. 100C3 = 100! / (100 – 3)! 3! = 100 * 99 * 98 / 3 * 2 = 161700.
Rearranging Letters
As a refresher, the formula for permutations (nPr) is: n! / (n – r)! And the formula for combinations (nCr) is: n! / ((n – r)! r!)
Given the letters ZDGII, list the number of total combinations of two through five letters (the letters do not have to form real words, ID and DI are different, but ID and ID [with the other I] are the same). This is a relatively complex problem because there is no one formula that will work for the whole problem. So how is it possible to solve this?
One way to solve this type of problem is to list all the different combinations and count them. For example, the different combinations for two letters are: ZD, ZG, ZI, DZ, DG, DI, GZ, GD, GI, IZ, ID, IG, and II, which totals 13. This is an effective system but it takes a long time. Imagine listing out all the combinations for ten letters!
It is much easier to create formulas than to list out all the combinations. An easy way to create formulas for complex problems is first to break it down into smaller and simpler parts. For this particular problem, the first step would be to break it up between the combinations without the double I, and the combinations with the double I. Without the double I, the letters would be ZDG and I. For three letter words, there would be 4P3 (4 * 3 * 2) combinations, which equal 24. This is the first part of the problem. The next part is using the double I. With the double I, the word would be I?I (II and something else, hence the question mark). The question mark can be replaced with the other three letters (3P1), it can also be put in any of the three positions (II?, I?I, and ?II, 3 choose 2 = 3). So the formula for the part with the double I, is: 3P1 (3) * 3C2 (3) = 9. Add this to the first part (24) and the result is 33. So the total number of combinations of three-letter words using five letters with one double letter is 33.
The same formula will work for four letters. The first part (no double) is 4P4 (4 * 3 * 2 * 1) = 24. The second part is 3P2 (3 * 2) * 4C2 (4 * 3 * 2 * 1 / 2 * 1 * 2 * 1) = 6 * 6 = 36. The solution is the sum of both parts: 24 + 36 = 60.
The same formula won’t work for five letters because there are no combinations without the double I. However, the second part will still work, and that is 3P3 (6) * 5C2 (10) = 60.
Once the formula was discovered, the rest ran smoothly. This is something to keep in mind for approaching complex problems, start simple, and work up until the entire problem is completed.
Probability and Statistics
Probability is the predicted outcome of an event. If two dice are rolled, it is probable that they will not both show ones, which means that it is not likely (but definitely possible) that two ones are rolled. Probability is shown in several forms, either as a ratio (50:50), with percents (50%) or as a fraction (1/2). Fractions are the easiest to handle mathematically and this is what is used in this book. Probability is calculated by the number of favorable outcomes over the number of total outcomes, so the probability of flipping a head with one coin is: one favorable event (a head) over two total events (either heads or tails) = 1/2.
Statistics is simply gathered data. Statistics can be used to discover an approximate probability, for example one way of finding the probability of flipping a heads with one coin is to flip a coin several times and see what happens. The more times the coin is flipped, the more accurate the answer will be, because if the coin is flipped only three times, heads could come up twice, which means that the predicted probability of flipping a head would be 2/3 which is incorrect. Simply put, probability is the prediction of what will happen while statistics is what has already happened. A few examples of probability problems are below:
1. When a die is rolled, what is the probability that a four is on top? There is one favorable event (the four) and there are six total events (1 – 6), which equals 1/6.
2. When two dice are rolled, what is the probability of rolling a pair? Any pair is a favorable event, and there are six ways to get a pair (two 1’s, two 2’s, two 3’s, two 4’s, two 5’s, or two 6’s). There are 6 * 6 = 36 total outcomes (using the fundamental counting principle). So the probability of rolling a pair with two dice is: 6/36 = 1/6. Please see the appendix for more problems.
Dice Chart
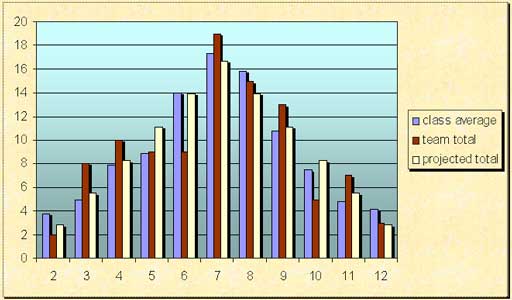
Our class split up into teams of three or four. Each team rolled a pair of dice one hundred times recording the sum of each roll. My teams’ rolls are illustrated in burgundy. Afterwards, my class averaged out all of our sums of the two dice (illustrated in blue). We noticed that the average of the class’ chart was much more constant than each teams’ average. We then calculated the likelihood of rolling each number (illustrated in yellow). This chart is the most constant of the three. From this we deduced that the more times something is recorded, the closer the chart of it is to the real probability.
Simple Dice Games
Casinos always play games that are in their favor. When the odds are in favor of one player over another it is called an “edge”. An example of a dice game is thus: the player pays ten cents per roll of one die. If a one, two or three is rolled, the player receives nothing. If the player rolls a five, the player receives fifteen cents. If a six is rolled, the player gets thirty cents. The trick of this game is that even though it seems that the player gets ten cents for rolling a four, he actually nets out even because he paid ten cents for that roll. So what the player actually nets for a roll is as follows: 1,2, or 3 = -10 cents; 4 = 0; 5 = 5 cents; 6 = 20 cents.
To find how big the edge is, first list how many combinations there are for each roll. There are six total possible rolls, which are 1, 2, 3, 4, 5, and 6. For one, two, and three, the player loses ten cents. So the first part of this equation is –30/6 (The player loses thirty cents out of six rolls). The next part is the four where the player breaks even, 0/6. The player makes five cents if he rolls a five, so this part is: 5/6. The player earns twenty cents for rolling a six, so this looks like this: 20/6. Add up all these numbers to find out how much the player earns in six rolls, -30/6 + 0/6 + 5/6 + 20/6 = -5/6. This means that in six rolls, the player loses five cents.
Another more complicated example is where the player again pays ten cents to play, and he rolls two dice. If the difference between the two dice is 0, 1, or 2, then he earns nothing. If the difference is 3, or 4, then he receives twenty cents (a net of ten). If the difference is five, then the player gets forty cents (a thirty cent net). It is a little more difficult to find the edge on this problem. There is a total of 6 * 6 = 36 number of rolls. The below chart shows all the possible rolls and what the difference is for each roll.
|
1 | 2 | 3 | 4 | 5 | 6 | |
|
|||||||
| 1 | |
0 | 1 | 2 | 3 | 4 | 5 |
| 2 | |
1 | 0 | 1 | 2 | 3 | 4 |
| 3 | |
2 | 1 | 0 | 1 | 2 | 3 |
| 4 | |
3 | 2 | 1 | 0 | 1 | 2 |
| 5 | |
4 | 3 | 2 | 1 | 0 | 1 |
| 6 | |
5 | 4 | 3 | 2 | 1 | 0 |
There are a total of 24 zeros, ones, and twos. The player loses ten cents for each of these rolls, so the equation for this is: -240/36. The player earns ten cents if he rolls a difference of three or four. There are ten ways to get a difference of three or four so this equation is: 100/36. When a difference of five is rolled, the player earns thirty cents. There are only two ways to get this, so this equation is: 60/36. The sum of these equations is: -240/36 + 100/36 + 60/36 = -80/36. So the player loses an average of eighty cents when he rolls thirty-six times.
To compare these two edges, change each denominator to one. The first edge is 5/6 and would be changed to: -5 divided by 6 = -0.83/1. The second edge would be: -80 divided by 36 = -2.22/1. The second edge is quite a bit larger than the first so it would be better to play the first game because the odds of winning are considerably higher though still not in the player’s favor.
Backgammon
A variation of backgammon is a game called Goose Girls and the Shepherd’s boys. This game board is 24 slots long with an end zone on either side. Each player has three pieces, which start in their end zones. The game board is split into four sections which each have special rules. The goal of the game is for a player to move all their pieces across the board and into their opponent’s end zone.
The game starts with both players rolling a die. The player who rolls highest goes first and uses that roll as their first turn. Players move a piece of their choice forward one space for each number shown on a die. The dice are used separately, so two pieces can be moved in a turn. For example, a roll of 3 - 4 says that either one piece is moved 3 spaces and another one 4, or one piece is moved 3 and 4 spaces forward making a total of 7 spaces. If a double is rolled, then the numbers shown on the dice are used four times. A double five means that four fives can be used, which can be split up between one, two or three pieces.
Pieces of the same color can share a space, but pieces of opposing colors cannot. However, if a piece lands on a space occupied by a single (not more than one) opposing piece, then the piece landed on is forced back to its end zone. Opposing pieces can move over one another without any extra action. Players must move all their pieces out of their end zones before moving any other piece. This means that at the start of the game, all three pieces must be put into play before a piece is moved twice and that if a piece is hit and put into the end zone, then it must be moved out first before any other piece is moved. All of a player’s pieces must be moved into an opposing players’ end zone before any of that player’s pieces can move off the board and out of the game.
In the board below, star piece can hit any of the lettered pieces. What is the probability of hitting the "A" piece? An easy way to solve this is to make a dice chart, which is illustrated below. The top row of the chart is the outcome of one die, and the side row is the outcome of the second die. The chart is the sum of the two dice. A way to solve the above problem would be to mark all the squares, which would satisfy the problem. For hitting the "A" only the rolls with a one in it would work. So the probability of hitting it would be: 11/36.
| * | A | B | C | D | E | F | ||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
To hit the "B" piece, any roll with four in it will work (11 combinations) and also, any roll that adds up to four (3 - 1, 2 - 2, 1 - 3). There is actually one more combination that will work, the double one. This will work because the one is used four times, which adds up to four. Now, each of these parts added together equals 15/36.
The rest of the probabilities can be found in the same way. The final list of probabilities for hitting each piece is as follows: A - 11/36, B - 15/36, C - 17/36, D - 6/36, E - 3/36, F - 3/36.
|
1 | 2 | 3 | 4 | 5 | 6 | |
|
|||||||
| 1 | |
2 | 3 | 4 | 5 | 6 | 7 |
| 2 | |
3 | 4 | 5 | 6 | 7 | 8 |
| 3 | |
4 | 5 | 6 | 7 | 8 | 9 |
| 4 | |
5 | 6 | 7 | 8 | 9 | 10 |
| 5 | |
6 | 7 | 8 | 9 | 10 | 11 |
| 6 | |
7 | 8 | 9 | 10 | 11 | 12 |
St. Olav's Random Miracle
In the eleventh century, King Olav of Norway and the King of Denmark had a dispute over the control of a small island. Diplomacy failed, so they waged a naval battle. During this battle while the nobility was socializing on a vantage point the two kings realized that they had the same amount of ships in the combat below. Rather than lose a sizable portion of their navies, several thousand warships, they agreed to settle their dispute over the throw of two dice. The king of Denmark rolled first. There was much ooh and ah-ing for the King had rolled a double six. King Olav however was a renowned dice player and with a smirk on his lips, he rolled the dice. While one of the dice landed with a six on top, the other cracked in two and one half landed with a six upturned while the other landed showing a one. The crowd stared at the dice gape-mouthed. The scholars declared this to be a work of god, and the King of Denmark proclaimed Olav the rightful owner of the island.
This true story is an example of an event occurring that is not listed in probability. While most of the time probability is correct, there will always be some erratic events. This is something that is good to keep in mind, that nothing is definite and that there are always exceptions.
Copyright © 2004 Daniel Parecki. All rights reserved.